Question

Joaquin and Trisha are playing a game in which the lower median wins the game. Their scores are shown below. Joaquin's scores: 75, 72, 85, 62, 58, 91 Trisha's scores: 92, 90, 55, 76, 91, 74 Which supports the conclusion that Joaquin won the game?

Answer 1

the answer is A)

Explanation:

took the test and got a 90

Answer 2

Explanation:

Given

Joaquin's score is
`75,72,85,62,58,91`

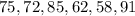
and Trisha's score is
`92,90,55,76,91,74`

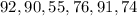
Arranging score in order of value we get

Joaquin's :
`58,62,72,75,85,91`

Trisha's :
`55,74,76,90,91,92`

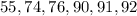
as no of values is even therefore their median is

Joaquin's
`=(72+75)/(2)=73.5`

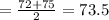
Trisha's
`=(76+90)/(2)=83`

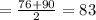
Therefore median of Joaquin's is lower

Thus Joaquin wins the game