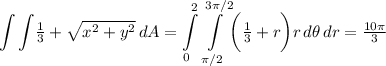Question

Sketch the region of integration and evaluate the following integral. ModifyingBelow Integral from nothing to nothing Integral from nothing to nothing With Upper R StartFraction 1 Over 3 plus StartRoot x squared plus y squared EndRoot EndFraction dA ​, RequalsStartSet (r comma theta ): 0 less than or equals r less than or equals 2 comma StartFraction pi Over 2 EndFraction less than or equals theta less than or equals StartFraction 3 pi Over 2 EndFraction EndSet

Answer 1

`(10\pi)/(3)`

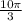
Explanation:

According to the information of the problem we have to compute the following integral.

`{\displaystyle \int\limits \int} (1)/(3) + √(x^2 + y^2) \, dA`

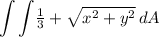
Where the region of integration is

`R = \Big\{ (r,\theta) : 0 \leq r \leq 2 , \,\,\,\, (\pi)/(2) \leq \theta \leq (3\pi)/(2) \Big\}`

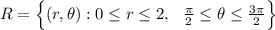
If you plot, that is just a circle between
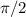`\pi/2` and
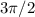`3\pi/2`, which is just half of the circle on the negative part of the plane.

When you switch coordinates

`{\displaystyle \int\limits \int} (1)/(3) + √(x^2 + y^2) \, dA = {\displaystyle \int\limits_(0)^(2) \int\limits_(\pi/2)^(3\pi/2)} \bigg((1)/(3) + r \bigg)r \, d\theta\, dr = (10\pi)/(3)`