Question

5 in
Q
2 in
R
PQ =
Using Pythagorean theorem

Answer 1

PQ^2 = QR^2 + PR^2

PQ^2 = 2^2 + 5^2

PQ^2 = 29

PQ = square root (29)

PQ = 5.3851648071

Explanation:

Answer 2

By applying Pythagorean's theorem to right-angled triangle PQR, the length of segment PQ is equal to
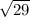`√(29)` units.

In Mathematics and Geometry, Pythagorean theorem is an Euclidean postulate that can be modeled or represented by the following mathematical equation:

`c^2=a^2+b^2`

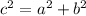
Where:

• a is the opposite side of a right-angled triangle.
• b is the adjacent side of a right-angled triangle.
• c is the hypotenuse of a right-angled triangle.

By applying Pythagorean's theorem to right-angled triangle PQR, the length of segment PQ can be calculated as follows;

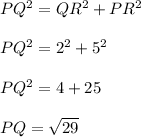`PQ^2=QR^2+PR^2\\\\PQ^2=2^2+5^2\\\\PQ^2=4 + 25\\\\PQ=√(29)`units.