Question

"We keep tossing a fair coin n = 10^6 million times, write down the outcomes: it gives a Heads-and-Tails-sequence of length n. We call an integer i special, if the i, i + 1, i + 2, i + 3, . . . , i + 18-th elements of the sequence are all Heads. That is, we have a block of 19 consecutive Heads starting with the i-th element of the sequence. Let X denote the number of special integers i. What is the expected value of X? I also want the numerical value. 5. We rand

Answer 1

Check the explanation

Explanation:

Let
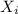`X_(i)` be the indicator random variable that takes the value 1 if the ith coin is the first coin in a sequence of 19 consecutive heads.

For any sequence of length 19, the starting coin can be from toss i ,

such that i is between 1 and n - 19+1

Thus the number of such sequences is

Kindly check the attached image below for the step by step explanation to the question above.