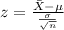Answer:
We define the random variable X as the walking age and we are interested if American children learn to walk less than 15 months so then that would be the alternative hypothesis and the complement would be the null hypothesis.
Null hypothesis:
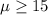
Alternative hypothesis:

And for this case the best answer would be:
H 0 : μ ≥ 15 vs. Ha : μ < 15
Explanation:
We define the random variable X as the walking age and we are interested if American children learn to walk less than 15 months so then that would be the alternative hypothesis and the complement would be the null hypothesis.
Null hypothesis:
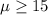
Alternative hypothesis:

And for this case the best answer would be:
H 0 : μ ≥ 15 vs. Ha : μ < 15
And the data given from the sample is:
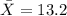 represent the sample mean
represent the sample mean
 represent the population deviation
represent the population deviation
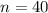 represent the sample size
represent the sample size
And the statistic would be given by: