Answer:
1. p = 14.63 lb/in² or 100890.608 Pa
2. p = 74676 Pa or 10.83 lb/in²
3. P = 2450 W or 3.28 hp
4.
 = 490105 N/m²
= 490105 N/m²
Step-by-step explanation:
1. Let's begin by listing out the given parameters:
density of mercury = 13.546 g/cm³ = 13546 kg/m³,
height of column = 76 cm = 0.76 m, acceleration due to gravity = 9.8m/s²
Using Pressure = density * acceleration due to gravity * height of column
p = ρ g h = 13546 * 9.8 * 0.76
p = 100890.608 Pa
To get the answer in lb/in², divide by 6895
p = 100890.608 ÷ 6895 = 14.632
p = 14.63 lb/in²
2. Let's list out the parameters given:
density of water = 62.43 lbm/ft³ = 62.43 * 16.018 = 1000kg/m³,
height of column = 25 ft = 25 ÷ 3.281 = 7.62 m,
acceleration due to gravity = 9.8m/s²
Using Pressure = density * acceleration due to gravity * height of column
p = ρ g h = 1000 * 9.8 * 7.62
p = 74676 Pa
To convert from Pa to lb/in², divide by 6895
p = 74676 ÷ 6895
p = 10.83 lb/in²
3. Let's list out the parameters given:
mass flow rate (ṁ) = 10 kg/s,
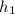 = 5 m,
= 5 m,
 = 30 m, Δh = 30 - 5 = 25 m, g = 9.8 m/s²
= 30 m, Δh = 30 - 5 = 25 m, g = 9.8 m/s²
Using Power = Energy (Potential Energy) ÷ Time
Energy (Potential Energy) = m g h
Power = mgΔh ÷ t; m÷ t = ṁ
Substitute ṁ into the equation
P = ṁ g h = 10 * 9.8 * 25
P = 2450 W
To convert from W to hp, divide by 746
P = 2450 ÷ 746 = 3.284
P = 3.28 hp
4. Let's list out the parameters given:
height (Δh) = 50 m, ṁ = 1 kg/s, g = 9.8 m/s²,
p2 = 105N/m², ρ = 1000 kg/m³
Using Bernoulli's Equation,
p1 + ½ρ(
 )² + ρgh1 = p2 + ½ρ(
)² + ρgh1 = p2 + ½ρ(
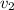 )² + ρgh2
)² + ρgh2
Assuming steady state flow;
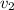 =
=
 ⇒
⇒
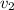 -
-
 = 0
= 0
 -
-
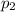 = ½ρ(
= ½ρ(
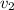 -
-
 )² + ρg(
)² + ρg(
 -
-
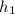 )
)
 -
-
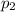 = ρgΔh
= ρgΔh
 - 105 = 1000 * 9.8 * 50
- 105 = 1000 * 9.8 * 50
 = 490000 + 105 = 490105
= 490000 + 105 = 490105
 = 490105 N/m²
= 490105 N/m²