Question

The GO transportation system of buses and commuter trains operates on the honor system. Train travelers are expected to buy their tickets before boarding the train. Only a small number of people will be checked on the train to see whether they bought a ticket. Suppose that a random sample of 200 train travelers was sampled and 24 of them had failed to buy a ticket. Estimate with 90% confidence the proportion of all train travelers who do not buy a ticket. Interpret the confidence interval you found.

Answer 1

The 90% confidence interval for the population proportion of all train travelers who do not buy a ticket is (0.08, 0.16).

Explanation:

The (1 - α)% confidence interval for the population proportion is:

`CI=\hat p\pm z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}`

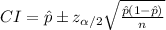
The information provided is:

n = 200

X = 24

Confidence level = 90%

Compute the value of sample proportion as follows:

`\hat p=(X)/(n)=(24)/(200)=0.12`

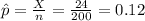
Compute the critical value of z for 90% confidence level as follows:

`z_(\alpha/2)=z_(0.10/2)=z_(0.05)=1.645`

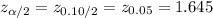
Compute the 90% confidence interval for the population proportion of all train travelers who do not buy a ticket as follows:

`CI=\hat p\pm z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}`

`=0.12\pm 1.645*\sqrt{(0.12(1-0.12))/(200)}\\\\=0.12\pm0.038\\=(0.082, 0.158)\\\approx (0.08, 0.16)`

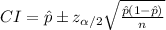
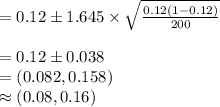
The 90% confidence interval for the population proportion of all train travelers who do not buy a ticket is (0.08, 0.16).

The 90% confidence interval (0.08, 0.16) for the population proportion of all train travelers who do not buy a ticket implies that there is a 0.90 probability that the true proportion lies in this interval.

Or if 100 such intervals are computed then 90 of those intervals will consist of the true proportion.