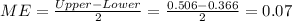Answer:
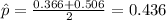
And the point of estimate for the proportion of employees who prefer plan is on this case 0.436 or 43.6%.
Explanation:
We define the parameter of interest as the proportion of employees who prefer plan p and we want to estimate this true parameter
The confidence interval for the this proportion is given by the following formula:
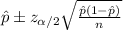
After calculate the 95% confidence interval we got (0.366, 0.506)
We can obtain the best estimate for the proportion of employees who prefer plan like this:
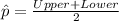
Where Upper and Lower represent the limits for the confidence interval and replacing we got:
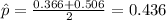
And the point of estimate for the proportion of employees who prefer plan is on this case 0.436 or 43.6%.
The margin of error can be estimated using the fact that this confidence interval is symmetrical and we got: