Question

horizontal circular platform rotates counterclockwise about its axis at the rate of 0.919 rad/s. You, with a mass of 73.5 kg, walk clockwise around the platform along its edge at the speed of "1.05" m/s with respect to the platform. Your 20.5 kg poodle also walks clockwise around the platform, but along a circle at half the platform's radius and at half your linear speed with respect to the platform. Your 18.5 kg mutt, on the other hand, sits still on the platform at a position that is 3/4 of the platform's radius from the center. Model the platform as a uniform disk with mass 90.7 kg and radius 1.91 m. Calculate the total angular momentum of the system

Answer 1

The total angular momentum is 292.59 kg.m/s

Step-by-step explanation:

Given that :

Rotation of the horizontal circular platform
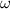`\omega` = 0.919 rad/s

mass of the platform (m) = 90.7 kg

radius (R) = 1.91 m

mass of the poodle
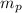`m_p` = 20.5 kg

Your mass
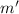`m'` = 73.5 kg

speed v = 1.05 m/s with respect to the platform

`V_p = (1.05)/(2) \ m /s \\ \\ = 0.525 \ m /s \\ \\r = (R)/(2)`

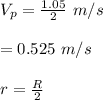
r = 0.955

Mass of the mutt
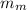`m_m` = 18.5 kg

`r' = (3)/(4) \ R`

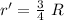
Your angular momentum is calculated as:

Your angular velocity relative to the platform is
`\omega' = (v)/(R) = (1.05)/(1.91 ) = 0.5497 \ rad/s`

`Actual \ \omega_y = \omega - \omega ' = (0.919 - 0.5497) \ rad/s = 0.3693 \ rad/s`

`I_y = m'R^2 = 73.5 *1.91^2= 268.14 \ kgm^2`

`L_Y = I_y*\omega_y= 268.14*0.3683= 98.76 \ kg.m/s`

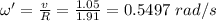
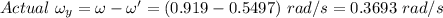
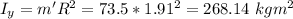
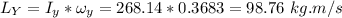
For poodle :

`Relative \ \ \omega' = (V_p)/(R/2) = 0.550 \ rad/s`

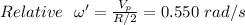
Actual
`\omega_p = \omega - \omega' = 0.919 -0.550 = 0.369 \ rad/s`

`I_p = m_p((R)/(2) )^2 = 20.5((1.91)/(2) )^2 = 18.70 \ kgm^2`

`L_p = I_p *\omega_p = 18.70*0.369 = 6.9003 \ kgm/s`

`I_M = m_m((3)/(y4) R)^2 = 18.5 ((3)/(4) 1.91)^2 = 37.96 \ kgm^2`

`L_M = I_M \omega = 37.96 * 0.919= 34.89 \ kg.m/s`

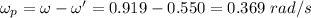
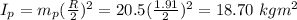
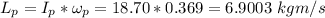
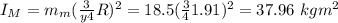
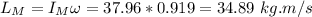
Disk
`I = (mr^2)/(2) = (90.7*1.91^2)/(2)= 165.44 \ kgm^2`

`L_D = I \omega = 165.44*0.919 =152.04 \ kg.m/s`

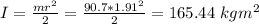
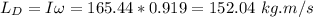
Total angular momentum of system is:

L =
`L_D +L_Y+L_P+L_M`

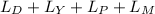
= (152.04 + 98.76 + 6.9003 + 34.89) kg.m/s

= 292.59 kg.m/s