Question

A national grocery store chain wants to test the difference in the average weight of turkeys sold in Detroit and the average weight of turkeys sold in Charlotte. According to the chain's researcher, a random sample of 20 turkeys sold at the chain's stores in Detroit yielded a sample mean of 17.53 pounds, with a sample standard deviation of 3.2 pounds. And a random sample of 24 turkeys sold at the chain's stores in Charlotte yielded a sample mean of 14.89 pounds, with a sample standard deviation of 2.7 pounds. Use a 5% level of significance to determine whether there is a difference in the mean weight of turkeys sold in these two cities. Assume the population variances are approximately the same and use the pooled t-test

Answer 1

Calculated value t = 1.3622 < 2.081 at 0.05 level of significance with 42 degrees of freedom

The null hypothesis is accepted .

Assume the population variances are approximately the same

Explanation:

Explanation:-

Given data a random sample of 20 turkeys sold at the chain's stores in Detroit yielded a sample mean of 17.53 pounds, with a sample standard deviation of 3.2 pounds

The first sample size 'n₁'= 20

mean of the first sample 'x₁⁻'= 17.53 pounds

standard deviation of first sample S₁ = 3.2 pounds

Given data a random sample of 24 turkeys sold at the chain's stores in Charlotte yielded a sample mean of 14.89 pounds, with a sample standard deviation of 2.7 pounds

The second sample size n₂ = 24

mean of the second sample "x₂⁻"= 14.89 pounds

standard deviation of second sample S₂ = 2.7 pounds

Null hypothesis:-H₀: The Population Variance are approximately same

Alternatively hypothesis: H₁:The Population Variance are approximately same

Level of significance ∝ =0.05

Degrees of freedom ν = n₁ +n₂ -2 =20+24-2 = 42

Test statistic :-

`t = \frac{x^(-) _(1) - x_(2) }{\sqrt{S^2((1)/(n_(1) ) }+(1)/(n_(2) ) }`

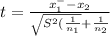
where
`S^(2) = (n_(1) S_(1) ^(2)+n_(2)S_(2) ^(2) )/(n_(1) +n_(2) -2)`

`S^(2) = (20X(3.2)^2+24X(2.7)^2)/(20+24-2)`

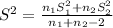
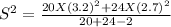
substitute values and we get S² = 40.988

`t= \frac{17.53-14.89 }{\sqrt{40.988((1)/(20) }+(1)/(24) )}`

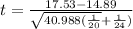
t = 1.3622

Calculated value t = 1.3622

Tabulated value 't' = 2.081

Calculated value t = 1.3622 < 2.081 at 0.05 level of significance with 42 degrees of freedom

Conclusion:-

The null hypothesis is accepted

Assume the population variances are approximately the same.