Answer:
The 99% of confidence limits for the proportion that plan to vote for the incumbent.
(0.6473 ,0.7527)
Explanation:
Explanation:-
Given data the election of a local construction union involves 2,000 union members. Among them, 500 members are randomly selected.
Given large sample size 'N' = 2000
Given sample size 'n' = 500
Given data Of the 500 surveyed, 350 said they would vote for the incumbent.
The sample Proportion
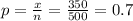
q = 1-p = 1 - 0.7 = 0.3
Confidence intervals:-
The 99% of confidence intervals are determined by

The z- score of 0.99 level of significance =2.576
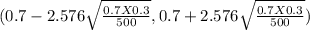
on using calculator, we get
(0.7 - 0.0527 ,0.7+0.0527)
(0.6473 ,0.7527)
Conclusion:-
The 99% of confidence limits for the proportion that plan to vote for the incumbent.
(0.6473 ,0.7527)