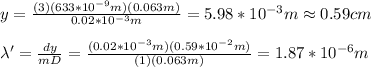Question

Two narrow slits 0.02 mm apart are illuminated by light from a CuAr laser (λ = 633 nm) onto a screen. a) If the first fringe is 0.2 cm away from the central fringe, what is the screen distance? b) What is the angle of the first dark fringe? c) How many fringes are visible? d) What wavelength would a laser have to provide a fringe that coincides (lines up) with the third order fringe of the CuAr laser?

Answer 1

a) 0.063m

b) 2.72°

c) 3151 fringes

d) 1.87*10^-6m

Step-by-step explanation:

a) To find the screen distance you use the following formula:

`y=(m\lambda D)/(d)\\\\D=(dy)/(m\lambda)`

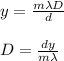
D: screen distance

d: distance between slits

m: order of the fringes

λ: wavelength

By replacing the values of the parameters you obtain:

`D=((0.02*10^(-3)m)(0.2*10^(-2)m))/((1)(633*10^(-9)m))=0.063m`

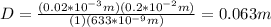
b) The condition for dark fringes is given by:

`\lambda(m+(1)/(2))=dsin\theta`

for the first dark fringe the angle is:

`\theta=sin^(-1)((\lambda(m+(1)/(2)))/(d))\\\\\theta=sin^(-1)(((633*10^(-9)m)(1+(1)/(2)))/(0.02*10^(-3)m))=2.72\°`

c) the visible number of fringes is given by:

`N=1+2(D)/(d)=1+(0.063m)/(0.02*10^(-3))=3151 \ fringes`

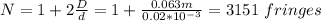
d) the wavelength of a laser in which its first order fringe coincides with the third one of the CuAr laser is:

`y=((3)(633*10^(-9)m)(0.063m))/(0.02*10^(-3)m)=5.98*10^(-3)m\approx0.59cm\\\\\lambda'=(dy)/(mD)=((0.02*10^(-3)m)(0.59*10^(-2)m))/((1)(0.063m))=1.87*10^(-6)m`