Question

A 300 MHz electromagnetic wave in air (medium 1) is normally incident on the planar boundary of a lossless dielectric medium with ϵr = 9 (medium 2). What is the wavelength of the incident wave and the wave in medium 2? What are the intrinsic impedances of media 1 and 2? What are the reflection coefficient and the transmission coefficient at the boundary? If the amplitude of the incident electric field is 10 V/m, what are the maximum amplitudes of the total fields in media 1 and 2? A standing wave pattern appears in medium 1. What are the locations of the first minimum and maximum?

Answer 1

Wavelength of the incident wave in air = 1 m

Wavelength of the incident wave in medium 2 = 0.33 m

Intrinsic impedance of media 1 = 377 ohms

Intrinsic impedance of media 2 = 125.68 ohms

Check the explanation section for a better understanding

Step-by-step explanation:

a) Wavelength of the incident wave in air

The frequency of the electromagnetic wave in air, f = 300 MHz = 3 * 10⁸ Hz

Speed of light in air, c = 3 * 10⁸ Hz

Wavelength of the incident wave in air:

`\lambda_(air) = (c)/(f) \\\lambda_(air) = (3 * 10^(8) )/(3 * 10^(8)) \\\lambda_(air) = 1 m`

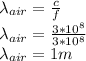
Wavelength of the incident wave in medium 2

The refractive index of air in the lossless dielectric medium:

`n = \sqrt{\epsilon_(r) } \\n = √(9 )\\n =3`

`\lambda_(2) = (c)/(nf)\\\lambda_(2) = (3 * 10^(6) )/(3 * 3 * 10^(6))\\\lambda_(2) = 1/3\\\lambda_(2) = 0.33 m`

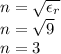
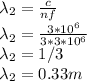
b) Intrinsic impedances of media 1 and media 2

The intrinsic impedance of media 1 is given as:

`n_1 = \sqrt{(\mu_0)/(\epsilon_(0) ) }`

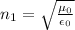
Permeability of free space,
`\mu_(0) = 4 \pi * 10^(-7) H/m`

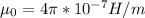
Permittivity for air,
`\epsilon_(0) = 8.84 * 10^(-12) F/m`

`n_1 = \sqrt{(4\pi * 10^(-7) )/(8.84 * 10^(-12) ) }`

`n_1 = 377 \Omega`

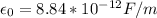
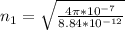
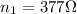
The intrinsic impedance of media 2 is given as:

`n_2 = \sqrt{(\mu_r \mu_0)/(\epsilon_r \epsilon_(0) ) }`

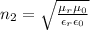
Permeability of free space,
`\mu_(0) = 4 \pi * 10^(-7) H/m`

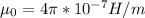
Permittivity for air,
`\epsilon_(0) = 8.84 * 10^(-12) F/m`

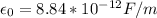
ϵr = 9

`n_2 = \sqrt{(4\pi * 10^(-7) *1 )/(8.84 * 10^(-12) *9 ) }`

`n_2 = 125.68 \Omega`

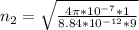
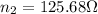
c) The reflection coefficient,r and the transmission coefficient,t at the boundary.

Reflection coefficient,
`r = (n - n_(0) )/(n + n_(0) )`

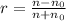
You didn't put the refractive index at the boundary in the question, you can substitute it into the formula above to find it.

`r = (3 - n_(0) )/(3 + n_(0) )`

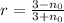
Transmission coefficient at the boundary, t = r -1

d) The amplitude of the incident electric field is
`E_(0) = 10 V/m`

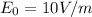
Maximum amplitudes in the total field is given by:

`E = tE_(0)` and
`E = r E_(0)`

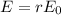
E = 10r, E = 10t