Answer:
Check the explanation
Explanation:
a)
the formula is given by,
c.v.=
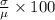
where is standard deviation and is mean of the given data.
b)for asse A,
c.v.=
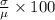 = 0.03 5 , 100 0,30 x 0.30 = 10%
= 0.03 5 , 100 0,30 x 0.30 = 10%
for asse B,
c.v.=
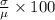 = 1.50 x 100 26005 × 100 =8.27 %
= 1.50 x 100 26005 × 100 =8.27 %
for asset C,
c.v.=
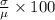 = 18.70 × 100 =10.71%
= 18.70 × 100 =10.71%
c)since, c.v. of asset B is least, it is least volatile and c.v. of asset is most, it is most volatile.