Question

A study was conducted to investigate the effectiveness of hypnotism in reducing pain. An SRS of 8 subjects was randomly selected, and the pain level was recorded for each one, with a lower score indicating less pain. After the subjects were hypnotized, their pain level was recorded again. The researchers calculated the difference in the pain level for each subject, calculated as After – Before. Assume the differences follow an approximately normal distribution, with the following sample statistics: Is pain, on average, lower after hypnotism? Test at a 1% significance level. a. The assumptions for this test are not met because the sample size is too small. b. Yes, the p-value is less than 0.01, so there is sufficient evidence at the 0.01 level to conclude that pain levels are lower after hypnotism. c. Yes, the p-value is greater than 0.01, so there is sufficient evidence at the 0.01 level to conclude that pain levels are lower after hypnotism. d. No, the p-value is less than 0.01, so there is insufficient evidence at the 0.01 level to conclude that pain levels are lower after hypnotism. e. No, the p-value is greater than 0.01, so there is insufficient evidence at the 0.01 level to conclude that pain levels are lower after hypnotism. 3 points Save Answer

Answer 1

e. No, the p-value is greater than 0.01, so there is insufficient evidence at the 0.01 level to conclude that pain levels are lower after hypnotism.

Explanation:

Hello!

The study's objective is to test if hypnotism reduces pain.

A sample of n=8 subjects was taken and the pain level was recorded in each subject before and after being hypnotized.

The variable of interest was determined by calculating the difference of pain level after - before hypnosis. This is a paired sample test and the variable can be determined as:

Xd: Difference between pain level felt after hypnosis and pain level felt before hypnosis of a subject.

The sample average and standard deviation obtained were:

Xd= -3

Sd= 3

And the variable is presumed to be approximately normal.

An approximately normal distribution is enough to conduct a paired sample t-test.

If the claim is that hypnosis reduces pain, then the average pain level after hypnosis should be less than the average pain level before hypnosis, then the average difference is expected to be negative, symbolically: μd < 0

The test will be one-tailed and so will be the p-value.

Remember: The p-value is defined as the probability corresponding to the calculated statistic if possible under the null hypothesis (i.e. the probability of obtaining a value as extreme as the value of the statistic under the null hypothesis).

So first step is to calculate the value of the statistic under the null hypothesis and then you can calculate the p-value.

H₀: μd ≥ 0

H₁: μd < 0

`t_(H_0)= (X_d-Mu_(d))/((S_d)/(n) )= (-0-0)/((3)/(√(8) ) ) = -2.828= -2.83`

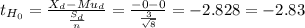
The DF of the t-test are n-1= 7

Then you can calculate the p-value as:

P(t₇≤-2.83)= 0.0127

The level of the test is α: 0.01

The decision rule is:

If p-value ≤ α, reject the null hypothesis.

If p-value > α, do not reject the null hypothesis.

The p-value > α the decision is to not reject the null hypothesis.

Correct option: e. No, the p-value is greater than 0.01, so there is insufficient evidence at the 0.01 level to conclude that pain levels are lower after hypnotism.

I hope this helps!