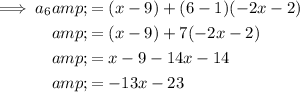Question

Find the 6th term of the arithmetic sequence X – 9, -X – 11, -3.3 – 13, ...

Answer 1

`-13x-23`

Explanation:

Given sequence:
`x-9, -x-11, -3x-13`

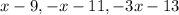
Therefore,

• 
  `a_1=x-9`
• 
  `a_2=-x-11`
• 
  `a_3=-3x-13`

General form of an arithmetic sequence:
`a_n=a+(n-1)d`

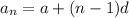
(where a is the first term and d is the common difference)

To find the common difference, subtract a term from the next term:

`\begin{aligned}d & =a_2-a_1\\ & =(-x-11)-(x-9)\\ & = -x-11-x+9\\ & = -2x-2\end{aligned}`

Therefore,

`a_n & =(x-9)+(n-1)(-2x-2)`

To find the 6th term, input n = 6 into the equation:

`\begin{aligned}\implies a_6 & =(x-9)+(6-1)(-2x-2)\\ & = (x-9)+7(-2x-2)\\ & = x-9-14x-14\\ & = -13x-23\end{aligned}`