Question

Determine whether the following probability experiment represents a binomial experiment and explain the reason for your answer. An investor randomly purchases 3 stocks listed on a stock exchange.​ Historically, the probability that a stock listed on this exchange will increase in value over the course of a year is 49​%. The number of stocks that increase in value is recorded.

Answer 1

The probability experiment represents a binomial experiment

Explanation:

On a Binomial experiment we have the following:

• There are n identical experiment
• Every experiment has 2 possibilities: success or fail
• There is a probability p of success and (1-p) of fail
• Every experiment is independent

Therefore, the probability experiment represents a binomial experiment because we have:

• The investor purchases 3 stocks listed on a stock exchange
• Every stock has 2 possibilities: increase in value over the course of a year or doesn't increase in value over the course of a year
• There is a probability of 0.49 that the stock increase in value over the course of a year and a probability of (1-0.49) that the stock doesn't increase in value over the course of a year
• The probability that every stock listed on this exchange increase in value over the course of a year is independent.

So, the probability that x stocks from the 3 that the investor purchases increase in value over the course of a year is equal to:

`P(x)=(n!)/(x!(n-x)!)*p^(x)*(1-p)^(n-x) \\P(x)=(3!)/(x!(3-x)!)*0.49^(x)*(1-0.49)^(3-x)`

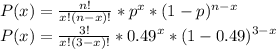
Where n is 3, and p is 0.49