Question

The following measurements were recorded for the drying time, in hours, of a certain brand of latex paint: 3.4, 2.5, 4.8, 2.9, 3.6, 2.8, 3.3, 5.6, 3.7, 2.8, 4.4, 4.0, 5.2, 3.0, 4.8. Assuming that the measurements represent a random sample from a normal population, find a 95% prediction interval for the drying time for the next trial of the paint.

Answer 1

The 95% confidence interval for the mean is (3.249, 4.324).

We can predict with 95% confidence that the next trial of the paint will be within 3.249 and 4.324.

Explanation:

We have to calculate a 95% confidence interval for the mean.

As the population standard deviation is not known, we will use the sample standard deviation as an estimation.

The sample mean is:

`M=(1)/(15)\sum_(i=1)^(15)(3.4+2.5+4.8+2.9+3.6+2.8+3.3+5.6+3.7+2.8+4.4+4+5.2+3+4.8)\\\\\\ M=(56.8)/(15)=3.787`

The sample standard deviation is:

`s=\sqrt{(1)/((n-1))\sum_(i=1)^(15)(x_i-M)^2}\\\\\\s=\sqrt{(1)/(14)\cdot [(3.4-(3.787))^2+(2.5-(3.787))^2+(4.8-(3.787))^2+...+(4.8-(3.787))^2]}\\\\\\`
`s=\sqrt{(1)/(14)\cdot [(0.15)+(1.66)+(1.03)+...+(1.03)]}`

`s=\sqrt{(13.197)/(14)}=√(0.9427)\\\\\\s=0.971`

We have to calculate a 95% confidence interval for the mean.

The population standard deviation is not known, so we have to estimate it from the sample standard deviation and use a t-students distribution to calculate the critical value.

The sample mean is M=3.787.

The sample size is N=15.

When σ is not known, s divided by the square root of N is used as an estimate of σM:

`s_M=(s)/(√(N))=(0.971)/(√(15))=(0.971)/(3.873)=0.2507`

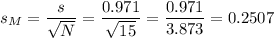
The t-value for a 95% confidence interval is t=2.145.

The margin of error (MOE) can be calculated as:

`MOE=t\cdot s_M=2.145 \cdot 0.2507=0.538`

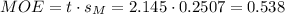
Then, the lower and upper bounds of the confidence interval are:

`LL=M-t \cdot s_M = 3.787-0.538=3.249\\\\UL=M+t \cdot s_M = 3.787+0.538=4.324`

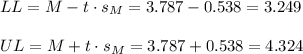
The 95% confidence interval for the mean is (3.249, 4.324).