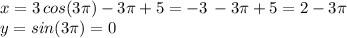Question

Graph the Plane Curve defined by:

x=3cos(t)−t+5, y=sin(t), for t in [0,3π]

Answer 1

Explanation:

Answer 2

Please see attached image for the graph

Explanation:

Give different values of "t" in radians, selecting those that can facilitate the calculation of sine and cosine. The values need to be in the interval from zero to
`3\,\pi`.

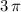Notice that for t = 0 we get :

`x=3\,cos(0)-0+5=3+5=8\\y=sin(0)=0`

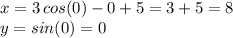
This is our initial point (8,0)

We can evaluate for
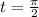`t=(\pi)/(2)` which also gives an easy to calculate value:

`x=3\,cos ((\pi)/(2) )-(\pi)/(2) +5=3*0-(\pi)/(2) +5=5-(\pi)/(2) \\y=sin((\pi)/(2) )=1`

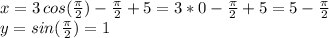
This point is the maximum reached by the curve on the first quadrant.

Another easy point is for
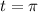`t=\pi`, which gives:

`x=3\,cos(\pi)-\pi+5=-3\,-\pi +5=2-\pi\\y=sin(\pi)=0`

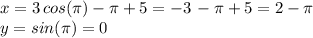
This is the crossing of the x-axis that we see to the left of the origin of coordinates.

The crossing of the x axis that appears then on the right of the origin of coordinates is when we use
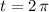`t=2\,\pi` (another simple to calculate point)

The minimum value reached by the graph (on the fourth quadrant) is obtained when we use
`t=(3\,\pi)/(2)`

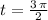
The maximum observed for the graph on the second quadrant is obtained when we use
`t=(5\,\pi)/(2)`.

And finally, the last point we obtained is when
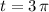`t=3\, \pi` which is the point where the graph stops on the left :

`x=3\,cos(3\pi)-3\pi+5=-3\,-3\pi +5=2-3\pi\\y=sin(3\pi)=0`