Question

The combined math and verbal scores for students taking a national standardized examination for college admission, is normally distributed with a mean of 820 and a standard deviation of 200. If a college requires a student to be in the top 15 % of students taking this test, what is the minimum score that such a student can obtain and still qualify for admission at the college calculator

Answer 1

Answer: 1007.28

Explanation:

Given : The combined math and verbal scores for students taking a national standardized examination for college admission, is normally distributed with

`\mu=820\ \ \ ,\ \sigma=200`

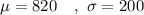
If a college requires a student to be in the top 15 % of students taking this test, it means that they want the students that score 85 percentile or above.

Let X be the scores of any random student, we require

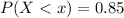`P(X<x)=0.85`, where x is minimum score that such a student can obtain and still qualify for admission at the college.

Formula for z-score =
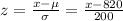`z=(x-\mu)/(\sigma)=(x-820)/(200)` ...(i)

From normal z-value table ,
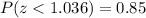`P(z<1.036)=0.85`...(ii)

From (i) and (ii) , we get

`(x-820)/(200)=1.0364\\\\\Rightarrow\ x-820=207.28\\\\\Rightarrow\ x=207.28+820=1007.28`

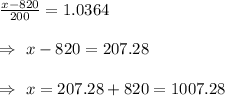
Hence, the minimum score that such a student can obtain and still qualify for admission at the college is 1007.28.