Answer:
Step-by-step explanation:
Given
Mass of block is

spring constant

Amplitude is
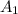
when putty is placed then amplitude decreases to
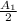
Initially
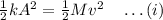
Conserving momentum
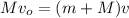
where
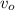 =initial velocity
=initial velocity
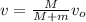
Now
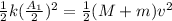
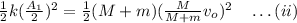
divide (i) and (ii) we get
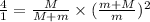
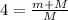

Fraction of energy converted into heat
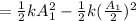
![=(1)/(2)kA_1^2[1-(1)/(4)]](https://img.qammunity.org/2021/formulas/physics/college/c79ky756deiywyfdo3b8wm3dfcclqdie4c.png)
![=(1)/(2)kA_1^2[0.75]](https://img.qammunity.org/2021/formulas/physics/college/8v1edvrc1tqrn7cpn6r95dr6yduecel5vr.png)
So,
 fraction is converted into heat energy
fraction is converted into heat energy