Answer:
6.25 days
Step-by-step explanation:
In order to compute the time first we have to find out the economic order quantity and the total number of orders in a year which is shown below:

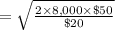
= 200 units
Now the total number of years in a year is
= Annual demand ÷ economic order quantity
= 8,000 ÷ 200 units
= 40 orders
And, the time between two consecutive orders is
= 1 ÷ 40 orders × 250 days
= 6.25 days