Question

The operations manager of a manufacturer of television remote controls wants to determine which batteries last the longest in his product. He took a random sample of his remote controls and tested two brands of batteries. Here are the number of minutes of continuous use before the batteries failed for each brand. Is there statistical evidence of a difference in longevity between the two batteries?

Answer 1

There is not enough evidence to support the claim that the longevity of the two brand of batteries differs.

Explanation:

The question is incomplete:

The sample data for each battery is:

Battery 1: 106 111 109 105

Battery 2: 125 103 121 118

The mean and STD for the sample of battery 1 are:

`M_1=(1)/(4)\sum_(i=1)^(4)(106+111+109+105)\\\\\\ M_1=(431)/(4)=107.75`

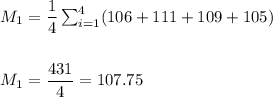
`s_1=\sqrt{(1)/((n-1))\sum_(i=1)^(4)(x_i-M)^2}\\\\\\s_1=\sqrt{(1)/(3)\cdot [(106-(107.75))^2+(111-(107.75))^2+(109-(107.75))^2+(105-(107.75))^2]}\\\\\\ s_1=\sqrt{(1)/(3)\cdot [(3.06)+(10.56)+(1.56)+(7.56)]}\\\\\\ s_1=\sqrt{(22.75)/(3)}=√(7.58333333333333)\\\\\\s_1=2.754`

The mean and STD for the sample of battery 2 are:

`M_2=(1)/(4)\sum_(i=1)^(4)(125+103+121+118)\\\\\\ M_2=(467)/(4)=116.75`

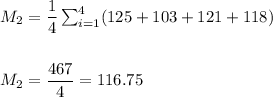
`s_2=\sqrt{(1)/((n-1))\sum_(i=1)^(4)(x_i-M)^2}\\\\\\s_2=\sqrt{(1)/(3)\cdot [(125-(116.75))^2+(103-(116.75))^2+(121-(116.75))^2+(118-(116.75))^2]}\\\\\\ s_2=\sqrt{(1)/(3)\cdot [(68.06)+(189.06)+(18.06)+(1.56)]}\\\\\\ s_2=\sqrt{(276.75)/(3)}=√(92.25)\\\\\\s_2=9.605`

This is a hypothesis test for the difference between populations means.

The claim is that the longevity of the two brand of batteries differs.

Then, the null and alternative hypothesis are:

`H_0: \mu_1-\mu_2=0\\\\H_a:\mu_1-\mu_2\\eq 0`

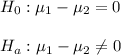
The significance level is α=0.05.

The sample 1, of size n1=4 has a mean of 107.75 and a standard deviation of 2.754.

The sample 2, of size n2=4 has a mean of 116.75 and a standard deviation of 9.605.

The difference between sample means is Md=-9.

`M_d=M_1-M_2=107.75-116.75=-9`

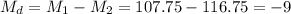
The estimated standard error of the difference between means is computed using the formula:

`s_(M_d)=\sqrt{(\sigma_1^2+\sigma_2^2)/(n)}=\sqrt{(2.754^2+9.605^2)/(4)}\\\\\\s_(M_d)=\sqrt{(99.841)/(4)}=√(24.96)=4.996`

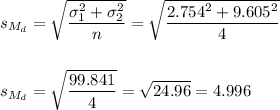
Then, we can calculate the t-statistic as:

`t=(M_d-(\mu_1-\mu_2))/(s_(M_d))=(-9-0)/(4.996)=(-9)/(4.996)=-1.8014`

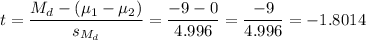
The degrees of freedom for this test are:

`df=n_1+n_2-1=4+4-2=6`

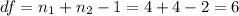
This test is a two-tailed test, with 6 degrees of freedom and t=-1.8014, so the P-value for this test is calculated as (using a t-table):

`P-value=2\cdot P(t<-1.8014)=0.122`

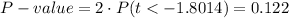
As the P-value (0.122) is greater than the significance level (0.05), the effect is not significant.

The null hypothesis failed to be rejected.

There is not enough evidence to support the claim that the longevity of the two brand of batteries differs.