Question

Teachers’ salaries in one state are very low that the educators in that state regularly complain about their compensation. The state mean is $33,600, but teachers in one district claim that the mean their district is significantly lower. They survey a simple random sample of 22 teachers in the district and calculate a mean salary of $32,400 with a standard deviation s = $ 1520. Test the teachers’ claim at the 0.05 level of significance.

Answer 1

`t=(32400-33600)/((1520)/(√(22)))=-3.702`

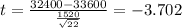
The degrees of freedom are given by:

`df=n-1=22-1=21`

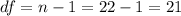
The p value is given by:

`p_v =P(t_((21))<-3.702)=0.00066`

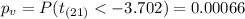
The p value is significantly lower than the significance level so then we have enough evidence to conclude that the true mean is significantly lower from 33600

Explanation:

Information given

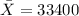`\bar X=33400` represent the sample mean

`s=1520` represent the sample standard deviation

`n=22` sample size

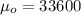`\mu_o =33600` represent the value that we want to analyze

`\alpha=0.05` represent the significance level

t would represent the statistic

`p_v` represent the p value for the test

System of hypothesis

We want to check if the true mean is lower than 33600, the system of hypothesis would be:

Null hypothesis:
`\mu \geq 33600`

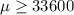
Alternative hypothesis:
`\mu < 33600`

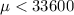
The statistic is given:

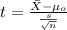`t=(\bar X-\mu_o)/((s)/(√(n)))` (1)

Replacing the data given we got:

`t=(32400-33600)/((1520)/(√(22)))=-3.702`

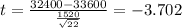
The degrees of freedom are given by:

`df=n-1=22-1=21`

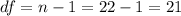
The p value is given by:

`p_v =P(t_((21))<-3.702)=0.00066`

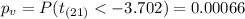
The p value is significantly lower than the significance level so then we have enough evidence to conclude that the true mean is significantly lower from 33600