Question

The Bureau of the Census reports the average commuting time for citizens of both Baltimore, Maryland, and Miami, Florida. To see if their commuting times appear to be any different in the winter, random samples of 40 drivers were surveyed in each city and the average commuting time for the month of January was calculated for both cities. The results are provided below. Miami (X1) Baltimore (X2) Sample size 40 40 Sample mean 28.5 min 35.2 min Population standard deviation 7.2 min 9.1 min At the 0.05 level of significance, can it be concluded that the commuting times are different in the winter? What is the test statistic? Round to 3 decimal places.

Answer 1

`z=\frac{28.5-35.2}{\sqrt{(7.2^2)/(40)+(9.1^2)/(40)}}}=-3.652`

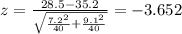
Now we can calculate the p value since we are conducting a bilateral test the p value would be:

`p_v =2*P(z<-3.652)=0.00026`

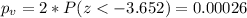
Since the p value is very low we have enough evidence to reject the null hypothesis that the true means are equal at 5% of significance.

Explanation:

Information provided

`\bar X_(1)=28.5` represent the mean for Miami

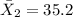`\bar X_(2)=35.2` represent the mean for Baltimore

`\sigma_(1)=7.2` represent the population standard deviation for Miami

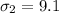`\sigma_(2)=9.1` represent the population standard deviation for Baltimore

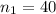`n_(1)=40` sample size selected for Miami

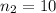`n_(2)=10` sample size selected for Baltimore

`\alpha=0.05` represent the significance level

z would represent the statistic (variable of interest)

`p_v` represent the p value for the test

Hypothesis to analyze

We want to check if the commiting times are different in the winter for the two cities, so then the system of hypothesis are:

Null hypothesis:
`\mu_(1) = \mu_(2)`

Alternative hypothesis:
`\mu_(1) \\eq \mu_(2)`

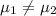
Since we know the population deviations the statistic for this case is given by:

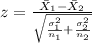`z=\frac{\bar X_(1)-\bar X_(2)}{\sqrt{(\sigma^2_(1))/(n_(1))+(\sigma^2_(2))/(n_(2))}}` (1)

Replacing the info provided we got:

`z=\frac{28.5-35.2}{\sqrt{(7.2^2)/(40)+(9.1^2)/(40)}}}=-3.652`

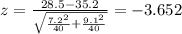
Now we can calculate the p value since we are conducting a bilateral test the p value would be:

`p_v =2*P(z<-3.652)=0.00026`

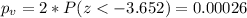
Since the p value is very low we have enough evidence to reject the null hypothesis that the true means are equal at 5% of significance.