Answer:
80% confidence interval for the proportion of homes that are "eclectic" is [0.59 , 0.78].
Explanation:
We are given that James takes a random sample of 42 homes form the Austin MLS (that's where Realtors go for information) and finds that 29 of them are listed as "eclectic" style.
Firstly, the pivotal quantity for 80% confidence interval for the population proportion is given by;
P.Q. =
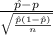 ~ N(0,1)
~ N(0,1)
where,
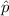 = sample proportion of homes that are "eclectic" =
= sample proportion of homes that are "eclectic" =
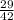 = 0.69
= 0.69
n = sample of homes = 42
 = population proportion of homes that are "eclectic"
= population proportion of homes that are "eclectic"
Here for constructing 80% confidence interval we have used One-sample z proportion statistics.
So, 80% confidence interval for the population proportion, p is ;
P(-1.282 < N(0,1) < 1.282) = 0.80 {As the critical value of z at 10% level
of significance are -1.282 & 1.282}
P(-1.282 <
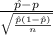 < 1.282) = 0.80
< 1.282) = 0.80
P(
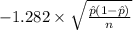 <
<
 <
<
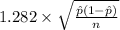 ) = 0.80
) = 0.80
P(
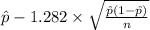 < p <
< p <
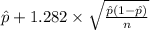 ) = 0.80
) = 0.80
80% confidence interval for p = [
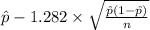 ,
,
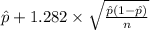 ]
]
= [
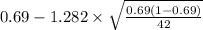 ,
,
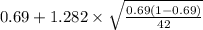 ]
]
= [0.59 , 0.78]
Therefore, 80% confidence interval for the proportion of homes that are "eclectic" is [0.59 , 0.78].