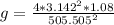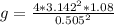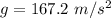Complete Question
The spaceship Intergalactica lands on the surface of the uninhabited Pink Planet, which orbits a rather average star in the distant Garbanzo Galaxy. A scouting party sets out to explore. The party's leader–a physicist, naturally–immediately makes a determination of the acceleration due to gravity on the Pink Planet's surface by means of a simple pendulum of length 1.08m. She sets the pendulum swinging, and her collaborators carefully count 101 complete cycles of oscillation during 2.00×102 s. What is the result? acceleration due to gravity:acceleration due to gravity: m/s2
Answer:
The acceleration due to gravity is
Step-by-step explanation:
From the question we are told that
The length of the simple pendulum is

The number of cycles is

The time take is
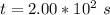
Generally the period of this oscillation is mathematically evaluated as
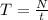
substituting values

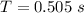
The period of this oscillation is mathematically represented as

making g the subject of the formula we have
![g = (L)/([(T)/(2 \pi ) ]^2 )](https://img.qammunity.org/2021/formulas/physics/college/yl7itecd2nx2xo45ejpbeikgjh57mnq6lk.png)
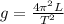
Substituting values