Question

corse hereo Joe has two drawers containing socks. The first contains three pairs of red socks, two pairs of black socks, and one pair of white socks. The second drawer contains two pairs of red socks, one pair of black socks, and two pairs of white socks. Each morning Joe flips a fair coin and picks two socks at random from the first drawer if heads is flipped; if tails is flipped he instead picks two socks at random from the second drawer. Joe is observed leaving his house this morning wearing one red and one black sock. What is the probability he flipped heads today?

Answer 1

P(H/A) = 0.6716

Explanation:

Let's call H the event that Joe flipped heads, T the event that Joe flipped tails and A the event that Joe wear one read and one black sock.

So, the probability that he flipped heads given that Joe wears one read and one black sock is calculated as:

P(H/A) = P(H∩A)/P(A)

Where P(A) = P(H∩A) + P(T∩A)

On the other hand, nCx gives the number of combinations in which we can select x elements from a group of n elements. nCx is calculated as:

`nCx=(n!)/(x!(n-x)!)`

So, the probability that Joe wear one red and one black sock given that he picks the socks from the first drawer is:

`(6C1*4C1*2C0)/(12C2)=0.3636`

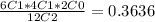
Because he need to choose one red sock from the 6 that are in the first drawer, one black sock from the 4 that are in the first drawer and 0 white socks. Additionally there are 12C2 ways to choose a pair of socks.

Therefore the probability P(H∩A) that that Joe flipped heads and Joe wear one read and one black sock is:

P(H∩A) = 0.5*0.3636 = 0.1818

Because there is a probability of 0.5 to flipped heads and the probability that Joe wear one red and one black sock given that he flipped heads is 0.3636.

At the same way, the probability that Joe wear one red and one black sock given that he picks the socks from the second drawer is:

`(4C1*2C1*4C0)/(10C2)=0.1778`

Therefore the probability P(T∩A) that that Joe flipped tails and Joe wear one read and one black sock is:

P(T∩A) = 0.5 * 0.1778 = 0.0889

Finally, P(A) and P(H/A) is equal to:

P(A) = 0.1818 + 0.0889 = 0.2707

P(H/A) = 0.1818/0.2707 = 0.6716