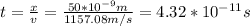Question

As computer structures get smaller and smaller, quantum rules start to create difficulties. Suppose electrons move through a channel in a microprocessor. If we know that an electron is somewhere along the 50 nm length of the channel, what is ∆vx? If we treat the elec- tron as a classical particle moving at a speed at the outer edge of the uncertainty range, how long would it take to traverse the channel?

Answer 1

a) ∆x∆v = 5.78*10^-5

∆v = 1157.08 m/s

b) 4.32*10^{-11}

Step-by-step explanation:

To solve this problem you use the Heisenberg's uncertainty principle, that is given by:

`\Delta x\Delta p \geq (\hbar)/(2)`

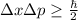
where h is the Planck's constant (6.62*10^-34 J s).

If you assume that the mass of the electron is constant you have:

`\Delta x \Delta (m_ev)=m_e\Delta x\Delta v \geq (\hbar)/(2)`

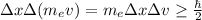
you use the value of the mass of an electron (9.61*10^-31 kg), and the uncertainty in the position of the electron (50nm), in order to calculate ∆x∆v and ∆v:

`\Delta x \Delta v\geq(\hbar)/(2m_e)=((1.055*10^(-34)Js))/(2(9.1*10^(-31)kg))=5.78*10^(-5)\ m^2/s`

`\Delta v\geq(5.78*10^(-5))/(50*10^(-9)m)=1157.08(m)/(s)`

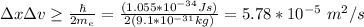
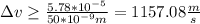
If the electron is a classical particle, the time it takes to traverse the channel is (by using the edge of the uncertainty in the velocity):

`t=(x)/(v)=(50*10^(-9)m)/(1157.08m/s)=4.32*10^(-11)s`