Question:
Suppose a simple random sample of size n = 1000 is obtained from a population whose size is N = 1,000,000 and whose population proportion with a specified characteristic is p = 0.44 . Complete parts (a) through (c) below.
(a) Describe the sampling distribution of ModifyingAbove p with caret.
A.)Approximately normal, mu Subscript ModifyingAbove p with caretequals0.44 and sigma Subscript ModifyingAbove p with caretalmost equals0.0002
B.)Approximately normal, mu Subscript ModifyingAbove p with caretequals0.44 and sigma Subscript ModifyingAbove p with caretalmost equals0.0005
C.)Approximately normal, mu Subscript ModifyingAbove p with caretequals0.44 and sigma Subscript ModifyingAbove p with caretalmost equals0.0157
(b) What is the probability of obtaining xequals480 or more individuals with the characteristic?
P(xgreater than or equals480)equals
nothing (Round to four decimal places as needed.)
(c) What is the probability of obtaining xequals410 or fewer individuals with the characteristic?
P(xless than or equals410)equals
nothing (Round to four decimal places as needed.)
Answer:
a) Option C.
b) 0.1021
c) 0.0280
Explanation:
Given:
Sample size, n = 1000
p' = 0.44
a) up' = p' = 0.44
The sampling distribution will be:
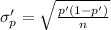
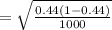
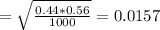
Option C is correct.
b) The probability when x ≥ 460
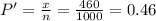
p'(P ≥ 0.46)
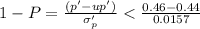

From the normal distribution table
NORMSDIST(1.27) = 0.898
1-0.8979 = 0.1021
Therefore, the probability = 0.102
c) x ≤ 410
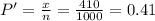
p'(P ≤ 0.41)
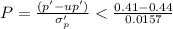

From the normal distribution table
NORMSDIST(-1.9108) = 0.0280
Probability = 0.0280