Question

Consider casting a concrete driveway 40 feet long, 12 feet wide and 6 in. thick. The proportions of the mix by weight are given as 1:2:3 for cement, sand, and gravel with w/c of 0.50. The specific gravities of sand and gravel are 2.60 and 2.70 respectively. Entrained air content is 7.5%. How many pounds of cement, water, sand, and gravel are needed for the driveway?

Answer 1

Answer:

Weight of cement = 10968 lb

Weight of sand = 18105.9 lb

Weight of gravel = 28203.55 lb

Weight of water = 5484 lb

Step-by-step explanation:

Given:

Entrained air = 7.5%

Length, L = 40 ft

Width,w = 12 ft

thickness,b= 6 inch, convert to ft = 6/12 = 0.5 ft

Specific gravity of sand = 2.60

Specific gravity of gravel = 2.70

The volume will be:

40 * 12 * 0.5 = 240 ft³

We need to find the dry volume of concrete.

Dry volume = wet volume * 1.54 (concrete)

Dry volume will be = 240 * 1.54 = 360ft³

Due to the 7% entarained air content, the required volume will be:

V = 360 * (1 - 0.07)

V = 334.8 ft³

At a ratio of 1:2:3 for cement, sand, and gravel respectively, we have:

Total of ratio = 1+2+3 = 6

Their respective volume will be =

Volume of cement =
`(1)/(6)*334.8 = 55.8 ft^3`

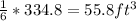
Volume of sand =
`(2)/(6)*334.8 = 111.6 ft^3`

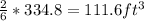
Volume of gravel =
`(3)/(6)*334.8 = 167.4 ft^3`

To find the pounds needed the driveway, we have:

Weight = volume *specific gravity * density of water

Specific gravity of cement = 3.15

Weight of cement =

55.8 * 3.15 * 62.4 = 10968 pounds

Weight of sand =

111.6 * 2.60 * 62.4 = 18105.9 lb

Weight of gravel =

167.4 * 2.7 * 62.4 = 28203.55 lb

Given water to cement ratio of 0.50

Weight of water = 0.5 of weight of cement

= 1/2 * 10968 = 5484 lb