Question

Answer the questions below about the function whose derivative is f prime (x )equalsStartFraction (x minus 2 )(x plus 8 )Over (x plus 1 )(x minus 5 )EndFraction ​, xnot equalsminus1​, 5. a. What are the critical points of​ f? b. On what open intervals is f increasing or​ decreasing? c. At what​ points, if​ any, does f assume local maximum and minimum​ values?

Answer 1

Explanation:

a) you have that:

`f'(x)=((x-2)(x+8))/((x+1)(x-5)),\ \ x\\eq -1,5`

The derivative of a function equals to zero allows you to find the critical points:

`f'(x)=0\\\\(x-2)(x+8)=0\\\\x_1=2\\\\x_2=-8`

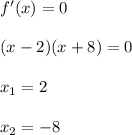
x=2,8 are the critical points

b) To know the behavior if f it is necessary to know where are f is indeterminated. The derivative give to you information about the slope of f. For x=-1,5 you have an infinite slope. Hence, for that values of x you have two indetermination s of f(x.)

However, if you see the atacched images you can obser that the original function (that is obtained with the intgegral) does not have available values for x<5 due to the logrithms. Hence, there are no critical points

The function only increases after x=5 from -infinity to +infinity

c) there are no local maximum neither local minimum