Answer:
Yes. At this significance level, there is evidence to support the claim that there is a difference in the ability of the brands to absorb water.
Explanation:
The question is incomplete:
The significance level is 0.05.
The data is:
Brand X: 91, 100, 88, 89
Brand Y: 99, 96, 94, 99
Brand Z: 83, 88, 89, 76
We have to check if there is a significant difference between the absorbency rating of each brand.
Null hypothesis: all means are equal
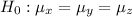
Alternative hypothesis: the means are not equal
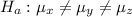
We have to apply a one-way ANOVA
We start by calculating the standard deviation for each brand:
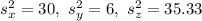
Then, we calculate the mean standard error (MSE):
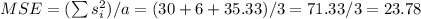
Now, we calculate the mean square between (MSB), but we previously have to know the sample means and the mean of the sample means:
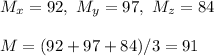
The MSB is then:

Now we calculate the F statistic as:
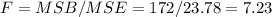
The degrees of freedom of the numerator are:
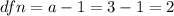
The degrees of freedom of the denominator are:
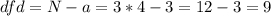
The P-value of F=7.23, dfn=2 and dfd=9 is:
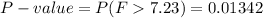
As the P-value (0.013) is smaller than the significance level (0.05), the null hypothesis is rejected.
There is evidence to support the claim that there is a difference in the ability of the brands to absorb water.