Question

. Block m1 slides along a frictionless surface at speed v1 = 4 m/s. Then it undergoes a onedimensional elastic collision with stationary block m2 = 2m1. Next, block m2 undergoes a one-dimensional elastic collision with stationary block m3 = 2m2. (a) What is the speed of block m3? Are the (b) speed, (c) kinetic energy, and (d) momentum of block m3 greater than, less than, or the same as the initial values for m1?

Answer 1

a) v3 = 1 m/s

c) K3 < K1

d) p3 = p1

Step-by-step explanation:

a) To solve this problem you use the conservation of the linear momentum in elastic collision.

In the first case you have:

`p_i=p_f\\\\m_1v_(1i)+m_2v_(2i)=m_1v_(1f)+m_2v_(2f)`

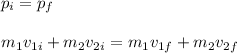
but the second block is at rest, then v2i = 0m/s:

`m_1v_(1i)=m_1v_(1f)+m_2v_(2f)`

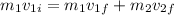
Furthermore, you can assume that the first object stops just after the collision with the second one. From this last expression you obtain the value of the second object:

`v_(2f)=(m_1v_(1i))/(m_2)\\\\m_2=2m_1\\\\v_(2f)=(m_1(4m/s))/(2m_1)=2\ m/s`

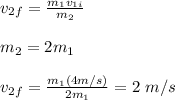
Then, you use the conservation of momentum for the second case, in which the second objects impact the third one:

`m_2v'_(2i)+m_3v_(3i)=m_2v'_(2f)+m_3v_(3f)\\\\v_(3i)=0\\\\m_2v'_(2i)=m_2v'_(2f)+m_3v_(3f)\\\\v_(2f)=0\\\\m_2v'_(2i)=m_3v_(3f)\\\\v_(3f)=(m_2v'_(2i))/(m_3)`

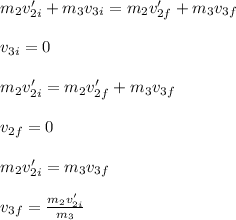
where again it has assumed that the second object stops, just after the impact with the third object. v'_2i = v_2f (in order to distinguish). BY using the fact m3 = 2m2 you obtain:

`v_(3f)=(m_2(2m/s))/(2m_2)=1\ m/s`

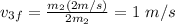
Then, you obtain that v3 < v2 < v1

c) The kinetic energy is given by:

`K=(1)/(2)mv^2`

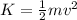
you compute for all the three objects:

`K_1=(1)/(2)m_1(4m/s)^2=8m_1\ m^2/s^2\\\\K_2=(1)/(2)m_2(2m/s)^2=(1)/(2)(2m_1)(4m^2/s^2)=4m_1\ m^2/s^2\\\\K_3=(1)/(2)m_3=(1m/s)^2=(1)/(2)(2m_2)(1\ m^2/s^2)=(1)/(2)(2(2m_1))(1 m^2/s^2)=2m_1\ m^2/s^2`

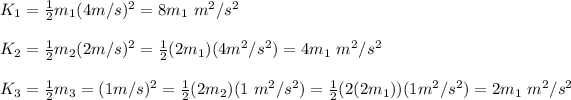
then, k3 < k2 < k1

d) For the momentum you have:

`p_1=4m_1\ m/s\\\\p_2=m_2(2m/s)=(2m_1)(2m/s)=4m_1\ m/s\\\\p_3=m_3(1m/s)=(2m_2)(1m/s)=(2(2m_1))(1m/s)=4m_1\ m/s`

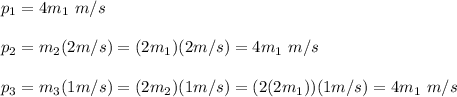
p1 = p2 = p3