Question

The diameters of computer parts made in a factory followed a normal distribution with a mean diameter of 6.5 inches and a standard deviation of 0.24 inches. The company considers all parts that are below the 16th percentile and all parts that are above the 84th percentile defective. What are the diameters of those defective parts? Show all of your work for full credit.

Answer 1

The diameters below 0.41 inches and above 0.89 inches are considered as defective.

Explanation:

Let X = diameters of computer parts.

The random variable X is normally distributed with mean, μ = 6.5 inches and standard deviation, σ = 0.24 inches.

The pth percentile is a data value such that at least p% of the data set is less than or equal to this data value and at least (100 - p)% of the data set are more than or equal to this data value.

Compute the 16th percentile of X as follows:

P (X < x) = 0.16

⇒ P (Z < z) = 0.16

The value of z for this probability is:

z = -0.99

Compute the value of x as follows:

`z=(x-\mu)/(\sigma)\\\\-0.99=(x-6.5)/(0.24)\\\\x=0.65-(0.99* 0.24)\\\\x=0.4124\\\\x\approx 0.41`

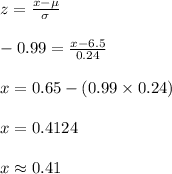
The value at the 16th percentile is 0.44 inches.

Compute the 84th percentile of X as follows:

P (X < x) = 0.84

⇒ P (Z < z) = 0.84

The value of z for this probability is:

z = 0.99

Compute the value of x as follows:

`z=(x-\mu)/(\sigma)\\\\0.99=(x-6.5)/(0.24)\\\\x=0.65+(0.99* 0.24)\\\\x=0.8876\\\\x\approx 0.89`

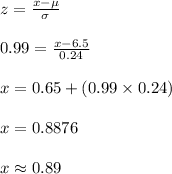
The value at the 84th percentile is 0.89 inches.

Thus, the diameters below 0.41 inches and above 0.89 inches are considered as defective.