to get the equation of any straight line, we simply need two points off of it, let's use those two points in the picture below.
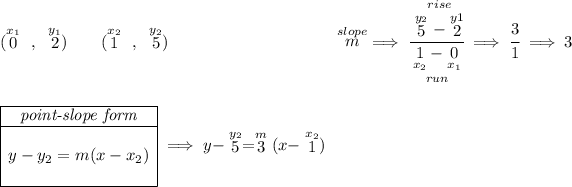
keeping in mind that for the point-slope form, either point will do, in this case we used the second one, but the first one would have worked just the same.