Answer:
99% confidence interval for the proportion of people who disagree with the statement is [0.667 , 0.713].
Explanation:
We are given that a survey that asked whether people agree or disagree with the statement ‘‘There is only one true love for each person." has been conducted. The result is that 735 of the 2625 respondents agreed, 1812 disagreed, and 78 answered ‘‘don’t know."
Firstly, the pivotal quantity for 99% confidence interval for the population proportion is given by;
P.Q. =
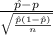 ~ N(0,1)
~ N(0,1)
where,
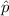 = sample proportion of people who disagree with the statement =
= sample proportion of people who disagree with the statement =
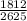 = 0.69
= 0.69
n = sample of respondents = 2625
p = population proportion of people who disagree with statement
Here for constructing 99% confidence interval we have used One-sample z proportion statistics.
So, 99% confidence interval for the population proportion, p is ;
P(-2.58 < N(0,1) < 2.58) = 0.99 {As the critical value of z at 0.5% level
of significance are -2.58 & 2.58}
P(-2.58 <
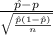 < 2.58) = 0.99
< 2.58) = 0.99
P(
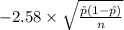 <
<
 <
<
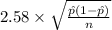 ) = 0.99
) = 0.99
P(
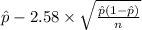 < p <
< p <
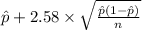 ) = 0.99
) = 0.99
99% confidence interval for p = [
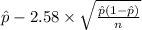 ,
,
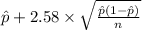 ]
]
= [
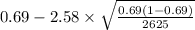 ,
,
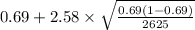 ]
]
= [0.667 , 0.713]
Therefore, 99% confidence interval for the proportion of people who disagree with the statement is [0.667 , 0.713].