Question

A sanitation department is interested in estimating the mean amount of garbage per bin for all bins in the city. In a random sample of 46 bins, the sample mean amount was 49.9 pounds and the sample standard deviation was 3.641 pounds. Construct a 95.7% confidence interval for the expected amount of garbage per bin for all bins in the city. Answer to 3 decimals (a) What is the lower limit of the 95.7% interval

Answer 1

The 95.7% confidence interval for the expected amount of garbage per bin for all bins in the city

(48.937 , 50.863)

Explanation:

Explanation:-

Given data random sample of 46 bins, the sample mean amount was 49.9 pounds and the sample standard deviation was 3.641

The sample size 'n' =46

mean of the sample x⁻ = 49.9

Standard deviation of the sample S = 3.641

Confidence intervals:-

The 95.7% confidence interval for the expected amount of garbage per bin for all bins in the city

`(x^(-) - t_(\alpha ) (S)/(√(n) ) ,x^(-) + t_(\alpha ) (S)/(√(n) ))`

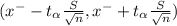
Degrees of freedom = n-1 = 46-1 =45

The tabulated value t₀.₉₆ = 1.794 ( from t-table)

`(49.9 - 1.794 (3.641)/(√(46) ) ,49.9+ 1.794 (3.641)/(√(46) ))`

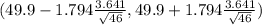
(49.9 -0.9630 , 49.9+0.9630)

(48.937 , 50.863)

Conclusion:-

The 95.7% confidence interval for the expected amount of garbage per bin for all bins in the city

(48.937 , 50.863)