We have been given that Mrs. Culland is finding the center of a circle whose equation is
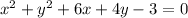 by completing the square. We are asked to find the final step of her work.
by completing the square. We are asked to find the final step of her work.
Let us complete the square.
We know that to complete square, we need to add the half the square of coefficient of x and y term.
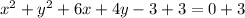
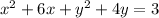
We can see that coefficient of x is 6 and coefficient of y is 4.
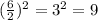
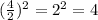
Now we will add 9 and 4 on both sides as:
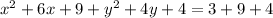
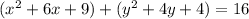
Now we will complete the square as:
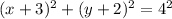
We know that standard form of equation of a circle is in form
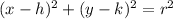 , where point (h,k) represents center of circle and r represents radius of circle.
, where point (h,k) represents center of circle and r represents radius of circle.
We can rewrite our equation as:
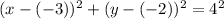
Now we can see that center is at point
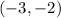 .
.
Therefore, the equation of the circle would be
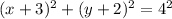 with a center at point
with a center at point
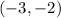 .
.