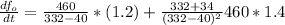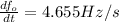Question

This is theDopplereffect. Sup-pose that, at a particular moment, you are in a train traveling at 34 m/s and acceleratingat 1.2m/s2. A train is approaching you from the opposite direction on the other trackat 40 m/s, accelerating at 1.4m/s2, and sounds its whistle, which has frequency of 460Hz. At that instant, what is the perceived frequency that you hear and how fast is itchanging

Answer 1

Complete Question

If a sound with frequency fs is produced by a source traveling along a line with speed vs and an observer is traveling with speed vo along the same line from the opposite direction toward the source, then the frequency of the sound heard by the observer is

f_o = [(c+v_o)/(c-v_s)] f_s

where c is the speed of sound, about 332 m/s. (This is the Doppler effect). Suppose that, at a particular moment, you are in a train traveling at 34 m/s and accelerating at 1.2 m/s^2. A train is approaching you from the opposite direction on the other track at 40 m/s, accelerating at 1.4 m/s^2, and sounds its whistle, which has a frequency of 460Hz. At that instant, what is the perceived frequency that you hear and how fast is it changing?

Answer:

The frequency the person hears is
`f_o = 557 Hz`

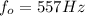
The speed at which it is changing is
`(df_o)/(dt) = 4.655 Hz/s`

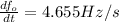
Step-by-step explanation:

Form the question we are told that

The frequency of the sound produced by source is
`f_s`

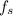
The speed of the source is
`v_s`

The speed of the observer

The frequency of sound heard by observer
`f_o =[ (c + v_o )/(c - v_s) ] * f_s`

The speed of sound is c with value
`c = 332 m/s`

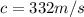
Looking the question we can deduce that the person in the first train is the observer so the

`v_o = 34 m/s`

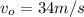
and the acceleration is
`(dv_o)/(dt) = 1.2 m/s^2`

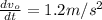
The train the travelling in the opposite direction the blew the whistle

is the source

So
`v_s = 40 m/s`

and
`f_s = 460 Hz`

and the acceleration is
`(dv_s)/(dt) = 1.4 m/s^2`

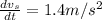
We are told that

`f_o =[ (c + v_o )/(c - v_s) ] * f_s`

Substituting values we have that

`f_o =[ (332 + 34 )/(332 - v40) ] * 460`

`f_o = 557 Hz`

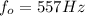
Differentiating
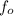`f_o` using chain rule we have that

`(d f_o)/(dt) = (df_o)/(dt ) * (dv_o)/(dt) + (d f_o)/(dv_s) * (dv_s)/(dt)`

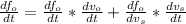
Now

`(df_o)/(dt ) = (f_s)/(c- v_s)`

`(df_o)/(dv_s) = (c+ v_o)/(c-v_s) f_s`

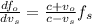
Substituting this into the equation

`(df_o)/(dt) = (f_s)/(c-v_s) * (d v_o)/(dt) + (c+v_o)/((c-v_s)^2) f_s * (dv_s)/(dt)`

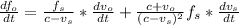
Now substituting values

`(df_o)/(dt) = (460)/(332 - 40) * (1.2) + (332+ 34)/((332- 40)^2) 460 * 1.4`

`(df_o)/(dt) = 4.655 Hz/s`