Question

American adults are watching significantly less television than they did in previous decades. In 2016, Nielsen reported that American adults are watching an average of five hours and twenty minutes, or 320 minutes, of television per day. 1. Find the probability that an average American adult watches more than 300 minutes of television per day. Answer in three decimal places. 2. Find the probability that an average American adult watches more than 2,000 minutes of television per week. Answer in three decimal places.

Answer 1

1. 0.869 = 86.9% probability that an average American adult watches more than 300 minutes of television per day.

2. 100% probability that an average American adult watches more than 2,000 minutes of television per week.

Explanation:

To solve this question, we need to understand the poisson distribution and the normal distribution.

Poisson distribution:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\lambda)*\lambda^(x))/((x)!)`

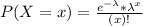
In which

x is the number of sucesses

e = 2.71828 is the Euler number

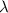`\lambda` is the mean in the given interval, which is the same as the variance.

Normal distribution:

Problems of normally distributed samples are solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

To approximate the Poisson to the normal, we use
`\mu = \lambda, \sigma = √(\lambda)`

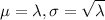
1. Find the probability that an average American adult watches more than 300 minutes of television per day.

The mean is 320 minutes per day, so
`\lambda = 320, \mu = 320, \sigma = √(320) = 17.89`

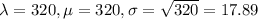
This probability is 1 subtracted by the pvalue of Z when X = 300. So

`Z = (X - \mu)/(\sigma)`

`Z = (300 - 320)/(17.89)`

`Z = -1.12`

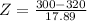
`Z = -1.12` has a pvalue of 0.131.

1 - 0.131 = 0.869

0.869 = 86.9% probability that an average American adult watches more than 300 minutes of television per day.

2. Find the probability that an average American adult watches more than 2,000 minutes of television per week.

A week has 7 days, so
`\lamda = 7*320 = 2240, \mu = 2240, \sigma = √(2240) = 47.33`

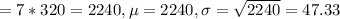
This probability is 1 subtracted by the pvalue of Z when X = 2000. So

`Z = (X - \mu)/(\sigma)`

`Z = (2000 - 2240)/(47.33)`

`Z = -5.07`

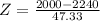
`Z = -5.07` has a pvalue of 0

1 - 0 = 1

100% probability that an average American adult watches more than 2,000 minutes of television per week.