Answer:
We are tryng to proof if more than half of all seniors think their job prospects are good so that would be the alternative hypothesis and the complement rule would be the null hypothesis.:
Null hypothesis:
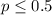
Alternative hypothesis:
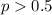
Explanation:
Information provided
n=100 represent the random sample ofcollege senior selected
X=53 represent the college seniors who say good
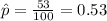 estimated proportion of seniors who think their job prospects are good
estimated proportion of seniors who think their job prospects are good
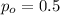 is the value that we want to test
is the value that we want to test
z would represent the statistic
 represent the p value
represent the p value
System of hypothesis
We are tryng to proof if more than half of all seniors think their job prospects are good so that would be the alternative hypothesis and the complement rule would be the null hypothesis.:
Null hypothesis:
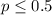
Alternative hypothesis:
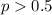
The statistic is given by:
 (1)
(1)
Replacing the info given we have:
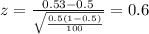
The p value for this case would be given by
