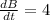Question

(e) The number of bees spotted in Amelie's garden can also be modeled by the function B(x) = 50√ k + 2x where x is the daily high temperature, in degrees Fahrenheit, and k is a positive constant. When the number of bees spotted is 100, the daily high temperature is increasing at a rate of 2 ◦F per day. According to this model, how quickly is the number of bees changing with respect to time when 100 bees are spotted?

Answer 1

`(dB)/(dt)=4`

Explanation:

Derivative indicates rate of change of dependent variable with respect to independent variables. It indicates the slope of a line that is tangent to the curve at the specific point.

Given:

Number of bees is modeled by the function
`B(x)=50√(k)+2x`

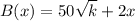
The daily high temperature is increasing at a rate of 2 °F per day when the number of bees spotted is 100.

To find:

rate of change of number of bees when 100 bees are spotted

Solution:

`B(x)=50√(k)+2x`

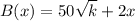
Differentiate with respect to t,

`(dB)/(dt)=0+2((dx)/(dt)) \\(dB)/(dt)=2((dx)/(dt)) \\`

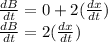
Put
`((dx)/(dt)) =2`

`(dB)/(dt)=2(2)=4`

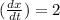
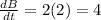
At x = 100,
`(dB)/(dt)=4`