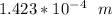Question

A cast-iron flywheel has a rim whose OD is 1.5 m and whose ID is 1.4 m. The flywheel weight should be chosen such that an energy fluctuation of 6.75 J will cause the angular speed to vary by no more than 240 to 260 rev/min. a.Estimate the coefficient of speed fluctuationb.If the weight of the spokes is neglected, determine the thickness of the rim

Answer 1

the coefficient of speed fluctuation is 0.08

the thickness of the rim is
`1.423*10^(-4)\ \ m`

Step-by-step explanation:

a.Estimate the coefficient of speed fluctuation

Let first determine the average speed of the flywheel by using the expression:

`n = (n_1+n_2)/(2)`

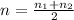
where;

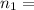`n_1 =` minimum speed = 240 rev/min

`n_2 =` maximum speed = 260 rev/min

∴
`n = (240 +260)/(2)`

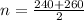
n = 250 rev/ min

To find the coefficient of speed fluctuation; we have:

`C_s = (n_2-n_1)/(n)`

`C_s = (260-240)/(250)`

`C_s = 0.08`

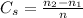
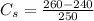
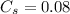
Hence; the coefficient of speed fluctuation is 0.08

b . If the weight of the spokes is neglected, determine the thickness of the rim

Let's start solving this process by finding the moment of inertia of the flywheel.

The moment of inertia of the fly wheel is given by the equation:

`I = \frac {E_2-E_1}{C_s \omega^2}`

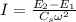
where ;

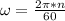`\omega = (2 \pi *n)/(60)` (since we are converting to rad/s)

`\omega = (2 \pi *250)/(60)`

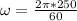
= 26.18 rad/s

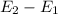`E_2-E_1` = the energy fluctuation = 6.75 J

`I = (6.75)/(0.08*26.18^2)`

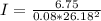
= 0.123 kg.m²

To determine the weight of the flywheel ; we have the following expression;

`I = (W)/(8g)(D^2+d^2)`

`W = (8gl)/(D^2_o+d_i^2)`

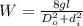
where;

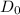`D_0` = outer diameter = 1.5 m

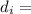`d_i =` inner diameter = 1.4 m

`W = (8*9.81*0.123)/(1.5^2+1.4^2)`

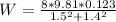
W = 2.29 N

Let employ the weight density of the cast-iron flywheel
`w \rho` = 70575.5N/m²

Then the volume of the flywheel:

`V = (W)/( w \ rho)`

`V = (2.29)/(70575.5)`

`V = 3.24*10^(-5) m^3`

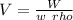
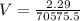
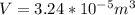
Let t be the thickness of the rim;

the thickness of the rim can be calculate by using the formula;

`V = (\pi t)/(4)(D^2-d^2)`

`t = (4V)/(\pi(D^2-d^2))`

`t = (4*3.24*10^(-5))/(\pi(1.5^2-1.4^2))`

`t = 1.423*10^(-4)m`

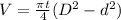
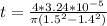
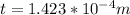
Hence, the thickness of the rim is
`1.423*10^(-4)\ \ m`