Answer:
67.5 square units
Explanation:
Formulae

(where b is the base and h is the height)

(where a and b are the bases, and h is the height)
Solution
We can divide this shape into a triangle and a trapezoid.
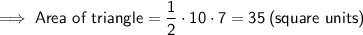
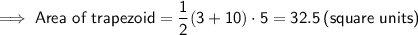
Therefore:
Area of shape = 35 + 32.5 = 67.5 square units