Question

A fully penetrating well in a 33 m thick confined aquifer pumps at a constant rate of 2000 m3/day for a long time. If the head in an observation well located160 m from the well is 249 m and the undisturbed head calculated at 453 m radius of influence is 250 m, determine the aquifer’s hydraulic conductivity (in m/d), transmissivity, and the drawdown 100 m away from the well. Problem

Answer 1

the aquifer’s hydraulic conductivity is K = 10.039 m/day

transmissivity T = 331.287 m/day

the drawdown 100 m away from the well is s = 1.452 m

Step-by-step explanation:

Given that :

The constant pumps rate Q = 2000 m³/day

R₁ =160 m → H₁ = 249 m

R₂ = 453 m → H₂ = 250 m

The confined aquifer B is 33 m thick

The hydraulic conductivity K =
`(Q*In ((R_1)/(R_2)) )/(2 \pi B(H_2-H_1))`

K =
`(2000*In ((160)/(453)) )/(2 \pi *33(250-249))`

K =
`(2081.43662)/(207.3451151)`

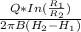
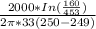
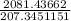
K = 10.039 m/day

Transmissivity T = K × B

T = 10.039×33

T = 331.287 m/day

TO find the drawdown 100 m away from the well; we have:

K =
`(Q* In((R_2)/(R_1) ))/(2 \pi B (H_2-H_1)) =(Q* In((R_2)/(R_3) ))/(2 \pi B (H_2-H_3))`

`( In((453)/(160) ))/((250-249)) =( In((453)/(100) ))/( (250-H_3))`

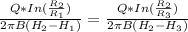
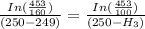
H₃ = 248.548 m

Drawdown (s) = H₂ - H₃

s = (250 - 248.548)m

s = 1.452 m