Final Answer:
The test statistic for the difference in proportions between the metropolitan area and the U.S. population is approximately ( -0.11 ). Since this value does not exceed the critical value of
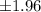 at the 0.05 significance level, there is insufficient evidence to conclude a significant difference. Therefore, we fail to reject the null hypothesis.
at the 0.05 significance level, there is insufficient evidence to conclude a significant difference. Therefore, we fail to reject the null hypothesis.
Explanation:
To determine whether there is sufficient evidence to conclude that a difference exists between this metropolitan area and the larger U.S. population, we can perform a hypothesis test for the difference in proportions.
Let:
 be the proportion of women in the metropolitan area.
be the proportion of women in the metropolitan area.
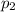 be the proportion of women in the larger U.S. population.
be the proportion of women in the larger U.S. population.
The null hypothesis
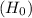 is that there is no difference between the proportions, and the alternative hypothesis
is that there is no difference between the proportions, and the alternative hypothesis
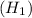 is that there is a significant difference.
is that there is a significant difference.
The formula for the test statistic for the difference in proportions ( z ) is given by:
![\[ z = \frac{(\hat{p}_1 - \hat{p}_2)}{\sqrt{p(1-p)\left((1)/(n_1) + (1)/(n_2)\right)}} \]](https://img.qammunity.org/2021/formulas/mathematics/college/cq79hkyqfow1f9pfwoi7qgy47v3f6fwlob.png)
Where:
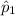 and
and
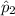 are the sample proportions of women in the metropolitan area and the U.S. population, respectively.
are the sample proportions of women in the metropolitan area and the U.S. population, respectively.
( p ) is the combined sample proportion.
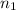 and
and
 are the sample sizes for the metropolitan area and the U.S. population, respectively.
are the sample sizes for the metropolitan area and the U.S. population, respectively.
First, let's calculate
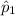 ,
,
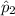 , ( p ), and then plug them into the formula to find the test statistic.
, ( p ), and then plug them into the formula to find the test statistic.
![\[ \hat{p}_1 = (112)/(150) = 0.7467 \]](https://img.qammunity.org/2021/formulas/mathematics/college/w9mxe5dp0i3qvsj5ls5gxk9he2s2vn1ws0.png)
![\[ \hat{p}_2 = (150)/(200) = 0.75 \]](https://img.qammunity.org/2021/formulas/mathematics/college/94ar3v5nbt1ojgob9c1egtizbfk0ew7gsh.png)
![\[ p = (112 + 150)/(150 + 200) = (262)/(350) = 0.7486 \]](https://img.qammunity.org/2021/formulas/mathematics/college/encqsxnmrygqwwnprsbmhc2pkgj054xezy.png)
Now, we can calculate the test statistic:
![\[ z = \frac{(0.7467 - 0.75)}{\sqrt{0.7486(1-0.7486)\left((1)/(150) + (1)/(200)\right)}} \]](https://img.qammunity.org/2021/formulas/mathematics/college/7c6o8no2rqsepctsethqigid6g0yaqj6d3.png)
Calculate the values and round the test statistic to two decimal places. If the absolute value of the test statistic is greater than the critical value for a two-tailed test at the 0.05 significance level, we reject the null hypothesis.
Note: The critical value for a two-tailed test at the 0.05 significance level is approximately
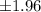 .
.