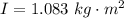Answer:
The rotational inertia of my wheel is
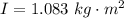
Step-by-step explanation:
From the question we are told that
The mass of the wheel is

The radius of the wheel is

The height is
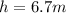
The linear speed is
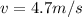
According to the law of energy conservation
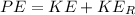
Where PE is the potential energy at the height h which is mathematically represented as
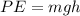
While KE is the kinetic energy at the bottom of height h
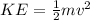
Where
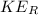 is the rotational kinetic energy which is mathematically represented as
is the rotational kinetic energy which is mathematically represented as
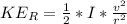
Where
 is the rotational inertia
is the rotational inertia
So substituting this formula into the equation of energy conservation
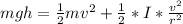
=>
![I =[ \ mgh - (1)/(2) mv^2 \ ]* (2 r^2)/(v^2)](https://img.qammunity.org/2021/formulas/physics/college/dqqwsy23ppfw47p7p950u90a1udmqzjsql.png)
substituting values
![I =[ \ 1.6 * 9.8 * 6.7 - (1)/(2) * 1.6 *4.7^2 \ ]* (2 * 0.37^2)/(4.7^2)](https://img.qammunity.org/2021/formulas/physics/college/5cefntn9f0xboaowdlyuca6zwebuqtaka4.png)