Question

The Census Bureau reports the average commute time for citizens of Cleveland, Ohio is 33 minutes. To see if the commute time is different in the winter, a random sample of 40 drivers were surveyed. The average commute time for the month of January was calculated to be 34.2 minutes and the population standard deviation is assumed to be 7.5 minutes. At the 0.05 level of significance, can it be concluded that the commuting times are different in the winter? What is the p-value? Use the rounded test statistic from the previous problem and round to 4 decimal places.

Answer 1

We conclude that the commuting times are same in the winter.

Explanation:

We are given that the Census Bureau reports the average commute time for citizens of Cleveland, Ohio is 33 minutes. To see if the commute time is different in the winter, a random sample of 40 drivers were surveyed.

The average commute time for the month of January was calculated to be 34.2 minutes and the population standard deviation is assumed to be 7.5 minutes.

Let
`\mu` = average commute time in winter.

So, Null Hypothesis,
`H_0` :
`\mu` = 33 minutes {means that the commuting times are same in the winter}

Alternate Hypothesis,
`H_A` :
`\mu`
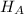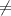`\\eq` 33 minutes {means that the commuting times are different in the winter}

The test statistics that would be used here One-sample z test statistics as we know about population standard deviation;

T.S. =
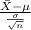`(\bar X-\mu)/((\sigma)/(√(n)))` ~ N(0,1)

where,
`\bar X` = sample mean commute time for the month of January = 34.2

`\sigma` = population standard deviation = 7.5 minutes

n = sample of drivers = 40

So, test statistics =
`(34.2-33)/((7.5)/(√(40)))`

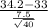
= 1.012

The value of z test statistics is 1.012.

Now, at 0.05 significance level the z table gives critical values of -1.96 and 1.96 for two-tailed test. Since our test statistics lies within the range of critical values of z, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region due to which we fail to reject our null hypothesis.

Therefore, we conclude that the commuting times are same in the winter.

Also, P-value of the test statistics is given by;

P-value = P(Z > 1.012) = 1 - P(Z
`\leq` 1.012)

= 1 - 0.84423 = 0.1558