Question

A Ferris wheel has a radius of 20 feet and is rotating at a rate of 4 revolutions per minute. When t = 0 (measured in seconds), a chair at the lowest point on the wheel is 6 feet above the ground. Write a model for the height, h, of the chair as a function of time.

Answer 1

the model for the height, h, of the chair at a function of time is
`y = -20 * sin ((2\pi )/(15) * t + (\pi )/(2) ) + 26`

Explanation:

To answer the question, we note that the height of the Ferris will varies proportionately to the angle of rotation, hence we can model the height according to he sine function as follows;

y = a·sin(b·x+c) + d

Where: a = Amplitude = Maximum displacement = r = 20 ft

or
`a = (maximum - minimum)/(2) = (44 - 4)/(2) = 20 \, ft`

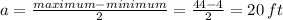
The period,
`(2\pi )/(b)` = Time for one complete revolution, for a Ferris wheel making 4 revolutions per minute, we have

Period = 1 minute/4 = 15 seconds

Therefore,
`(2\pi )/(b)` = 15 seconds or
`(b =(2\pi )/(15))`

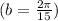
d = the vertical shift is given by minimum + amplitude or maximum - amplitude = 6 + 20 = 26 ft

c = Phase shift since we want the chair to be at the minimum at t = 0 we put c = π/2

x = Independent variable, which in the case of the question is time, t

Therefore, the model for the height, h, of the chair at a function of time is as follows

`y = -20 * sin ((2\pi )/(15) * t + (\pi )/(2) ) + 26`

i.e. y = -20×sin(2π/15 + π/2) + 26.